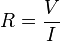Marco Teorico
Movimiento armónico simple
El movimiento armónico simple (se abrevia m.a.s.), también denominado movimiento vibratorio armónico simple
(abreviado m.v.a.s.), es un movimiento periódico, oscilatorio y vibratorio en ausencia de fricción, producido por la
acción de una fuerza recuperadora que es directamente proporcional al desplazamiento pero en sentido opuesto.
Y que queda descrito en función del tiempo por una función senoidal (seno o coseno).
Si la descripción de un movimiento requiriese más de una función armónica, en general sería un movimiento armónico,
pero no un m.a.s. En el caso de que la trayectoria sea rectilínea, la partícula que realiza un m.a.s. oscila alejándose
y acercándose de un punto, situado en el centro de su trayectoria, de tal manera que su posición en función del tiempo
con respecto a ese punto es una sinusoide. En este movimiento, la fuerza que actúa sobre la partícula es proporcional
a su desplazamiento respecto a dicho punto y dirigida hacia éste.


Péndulo simple
El péndulo simple o matemático es un sistema idealizado constituido por una partícula de masa
m que está suspendida de un punto fijo O mediante un hilo inextensible y sin peso. Naturalmente es
imposible la realización práctica de un péndulo simple, pero si es accesible a la teoría.
El péndulo simple o matemático se denomina así en contraposición a los péndulos reales,
compuestos o físicos, unicos que pueden construirse.

PERIODO DE OSCILACION
En física, el período de una oscilación u onda (T) es el tiempo transcurrido entre
dos puntos equivalentes de la onda. El concepto aparece tanto en matemáticas como
en física y otras áreas de conocimiento
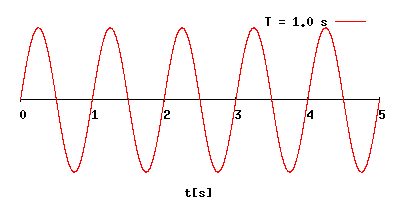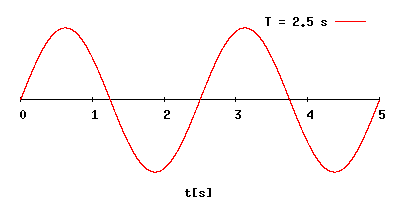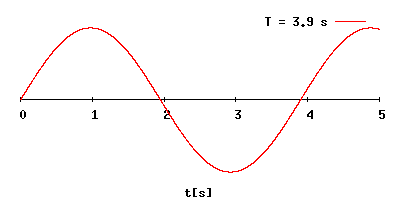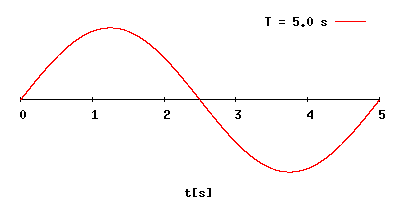
Es el mínimo lapso que separa dos instantes en los que el sistema se encuentra
exactamente en el mismo estado: mismas posiciones, mismas velocidades, mismas
amplitudes. Así, el periodo de oscilación de una onda es el tiempo empleado por la
misma en completar una longitud de onda. En términos breves es el tiempo que dura un
ciclo de la onda en volver a comenzar. Por ejemplo, en una onda, el periodo es el tiempo
transcurrido entre dos crestas o valles sucesivos. El periodo (T) es inverso a la frecuencia (f):
Como el periodo siempre es inverso a la frecuencia, la longitud de onda también está
elacionada con el periodo, mediante la fórmula de la velocidad de propagación. En este
caso la velocidad de propagación será el cociente entre la longitud de onda y el período.
En física un movimiento periódico siempre es un movimiento acotado, es decir, está
confinado a una región finita del espacio de la cual las partículas nunca salen. Un ejemplo
de ello es el movimiento unidimensional de una partícula por la acción de una fuerza
conservativa si  es el potencial asociado a la fuerza conservativa, para energías
es el potencial asociado a la fuerza conservativa, para energías
ligeramente superiores a un mínimo de energía  la partícula realizará un movimiento
la partícula realizará un movimiento
oscilatorio alrededor de de la posición de equilibrio dada por el mínimo local de energía.
El período de oscilación depende de la energía y viene dado por la expresión:1
MEDIDA DE ACELERACION DE LA GRAVEDAD
Cuando el ángulo q es pequeño entonces, senq » q , el péndulo describe oscilaciones armónicas
cuya ecuación es
q =q0·sen(w t+j )
de frecuencia angular w2=g/l, o de periodo
![]()
La ley de la gravitación de Newton describe la fuerza de atracción entre dos cuerpos de masas
M y m respectivamente cuyos centros están separados una distancia r.
La intensidad del campo gravitatorio g, o la aceleración de la gravedad en un punto P situado a una
distancia r del centro de un cuerpo celeste de masa M es la fuerza sobre la unidad de masag=F/m
colocada en dicho punto.
![]()
su dirección es radial y dirigida hacia el centro del cuerpo celeste.
En la página dedicada al estudio del Sistema Solar, proporcionamos los datos relativos a la masa
(o densidad) y radio de los distintos cuerpos celestes.
Ejemplo:
Marte tiene un radio de 3394 km y una masa de 0.11 masas terrestres (5.98·1024 kg). La aceleración g
de la gravedad en su superficie es
![]()
Tenemos dos procedimientos para medir esta aceleración
- Cinemática
Se mide con un cronómetro el tiempo t que tarda en caer una partícula desde una altura h. Se supone que
h es mucho más pequeña que el radio r del cuerpo celeste.
![]()
- Oscilaciones
Se emplea un instrumento mucho más manejable, un péndulo simple de longitud l. Se mide el periodo de varias
oscilaciones para minimizar el error de la medida y se calculan el periodo P de una oscilación. Finalmente, se
despeja g de la fórmula del periodo.
De la fórmula del periodo establecemos la siguiente relación lineal.
![]()
|
|
|
Se representan los datos "experimentales" en un sistema de ejes:
- P2/(4p2) en el eje vertical y
- La longitud del péndulo l en el eje horizontal.
La pendiente de la recta es la inversa de la aceleración de la gravedad S
SISTEMA MASA RESORTE

Otro ejemplo de Movimiento Armónico Simple es el sistema masa-resorte que
consiste en una masa “m” unida a un resorte, que a su vez se halla fijo a una
pared, como se muestra en la figura. Se supone movimiento sin rozamiento
sobre la superficie horizontal.

El resorte es un elemento muy común en máquinas. Tiene una longitud normal, en ausencia de fuerzas
externas. Cuando se le aplican fuerzas se deforma alargándose o acortándose en una magnitud “x”
llamada“deformación”. Cada resorte se caracteriza mediante una constante “k” que es igual a la fuerza
por unidad de deformación que hay que aplicarle. La fuerza que ejercerá el resorte es igual y opuesta a
la fuerza externa aplicada (si el resorte deformado está en reposo) y se llama fuerza recuperadora elástica.
Dicha fuerza recuperadora elástica es igual a :

En el primer dibujo tenemos el cuerpo de masa “m” en la posición de equilibrio, con el resorte teniendo su
longitud normal. Si mediante una fuerza externa lo apartamos de la misma (segundo dibujo), hasta una
deformación “x = + A” y luego lo soltamos, el cuerpo empezará a moverse con M.A.S. oscilando en torno
a la posición de equilibrio. En este dibujo la fuerza es máxima pero negativa, lo que indica que va hacia la
izquierda tratando de hacer regresar al cuerpo a la posición de equilibrio.
Llegará entonces hasta una deformación “x = -A” (tercer dibujo). En este caso la deformación negativa
indica que el resorte está comprimido. La fuerza será máxima pero positiva, tratando de volver al cuerpo
a su posición de equilibrio.
A través de la Segunda Ley de Newton relacionamos la fuerza actuante (recuperadora) con la aceleración a(t).


Cualidades Del Sonido & Las Cuerdas Sonoras

Cualidades del sonido :

El oído es capaz de distinguir unos sonidos de otros porque es sensible a las diferencias que puedan existir
entre ellos en lo que concierne a alguna de las tres cualidades que caracterizan todo sonido y que son la
intensidad, el tono y el timbre. Aun cuando todas ellas se refieren al sonido fisiológico, están relacionadas
con diferentes propiedades de las ondas sonoras.
intencidad
La intensidad del sonido percibido, o propiedad que hace que éste se capte como fuerte o como débil, está
relacionada con la intensidad de la onda sonora correspondiente, también llamada intensidad acústica.
La intensidad acústica es una magnitud que da idea de la cantidad de energía que está fluyendo por el
medio como consecuencia de la propagación de la onda.
Tono
El tono es la cualidad del sonido mediante la cual el oído le asigna un lugar en la escala musical, permitiendo,
por tanto, distinguir entre los graves y los agudos. La magnitud física que está asociada al tono es la frecuencia.
Los sonidos percibidos como graves corresponden a frecuencias bajas, mientras que los agudos son debidos a
frecuencias altas. Así el sonido más grave de una guitarra corresponde a una frecuencia de 82,4 Hz y el más
agudo a 698,5 hertzs.
Timbre
El timbre es la cualidad del sonido que permite distinguir sonidos procedentes de diferentes instrumentos, aun
cuando posean igual tono e intensidad. Debido a esta misma cualidad es posible reconocer a una persona por
su voz, que resulta característica de cada individuo.
Efecto Doppler

El efecto doppler se trata del cambio aparente en la frecuencia de una onda emitida por una fuente en movimiento.
El efecto doppler aplica tanto para las ondas mecánicas como para las ondas electromagnéticas. Además se utiliza
para determinar el movimiento de las estrellas. La luz de una estrella puede mostrar corrimiento hacia un extremo u
otro del espectro de luz visible. Este corrimiento evidencia si la estrella o galaxia se esta acercando o alejando de
nosotros. En esta lección nos enfocaremos en el efecto doppler aplicado al sonido.


Cuerdas Sonoras

Una cuerda es el elemento vibratorio que origina el sonido en los instrumentos musicales de cuerda, tales como la
guitarra, el arpa, el piano, el contrabajo o miembros de la familia de los violines, descendientes lejanos de las
antiguas vihuelas.
Las cuerdas son segmentos formados por un material flexible que permanecen en tensión de modo que puedan
vibrar libremente, sin entorpecimiento que provocase una distorsión de la onda acústica.
Las cuerdas pueden ser lisas, que constan de un material único como acero, nailon, oro o tripas de animales; o
bien pueden poseer un interior de seda, o nailon y entorchadas con hilos de acero, cobre, plata u oro en el caso
de las notas más agudas del violín. Este entorchado tiene la misión de añadir cierto peso y homogeneidad en la
vibración de modo que la cuerda alcance la altura sonora deseada, mientras la mantiene lo suficientemente delgada
y flexible para tocar.
Las cuerdas sonoras son medios elásticos que al ser excitados correctamente producirán un sonido.
las cuerdas presentan las siguientes características según el gráfico.
A= Husos
N= Nodos
L= Longitud de la cuerda
n= Numero de armónico.
Las cuerdas presentan frecuencias distintas dependiendo del numero de armónico al que deseemos calcular la frecuencia.
Formula general:
Fn= n* v / 2L
Donde:
Fn= Frecuencia n
n= numero de armonico
v= constante del sonido (340 m/s2)

Tubos Sonoros
Se llaman tubos sonoros aquellos que contienen una columna gaseosa (columna de aire) capaz de producir sonido al
ser convenientemente excitada. El cuerpo sonoro es la columna gaseosa, y no el tubo que la contiene; en efecto, éste
tiene la importante función de definir la forma de aquella pero fuera de esto, influye relativamente poco sobre los
fenómenos sonoros. Los tubos sonoros pueden ser cerrados, es decir, que poseen una sola abertura y tubos abiertos,
que poseen dos o más.
Vibración de la columna de aire contenida en un tubo
Las columnas de aire contenidas en los tubos sonoros se comportan, desde ciertos puntos de vista, como cuerdas
musicales, por lo tanto las columnas de aire vibrantes poseen nodos, o sea puntos donde la vibración es nula, y vientres,
equidistantes de los anteriores, donde la vibración alcanza su máxima amplitud.
La vibración de las columnas de aire es longitudinal; los nodos serán por tanto, puntos de condensación y los vientres
puntos de dilatación o rarefacción; en los extremos cerrados siempre se producen nodos y en los extremos abiertos
generalmente se producen vientres. El punto de excitación no puede ser un nodo, pero no necesita ser un vientre, pudiendo
estar en un punto intermedio. No es necesario que las aberturas de un tubo coincidan con los extremos, pudiendo éstos
estar cerrados y haber una o más aberturas en otras partes del tubo (la gaita).
Una columna de aire puede vibrar con toda su longitud o dividida en segmentos iguales lo mismo que las cuerdas; en el primer
caso se obtiene el sonido llamado fundamental, y en los otros los armónicos: segundo, si la columna vibra dividida en mitades;
tercero, si vibra en tercios, etc.
Tomando como punto de partida el que en los extremos de un tubo abierto, sólo pueden haber vientres de vibración, el tubo
producirá su fundamental cuando vibre con un nodo único en su centro. Cuando el tubo produce su segundo armónico,
producirá dos nodos y tres vientres; cuando produce su tercer amónico, producirá tres nodos y 4 vientres, y así sucesivamente.
Tubos Sonoros Cerrados

Tubos Sonoros abiertos

LA LUZ
e llama luz (del latín lux, lucis) a la parte de la radiación electromagnética que puede ser percibida por el ojo humano.
En física, el término luz se usa en un sentido más amplio e incluye todo el campo de la radiación conocido como
espectro electromagnético, mientras que la expresión luz visible señala específicamente la radiación en el espectro visible.
La óptica es la rama de la física que estudia el comportamiento de la luz, sus características y sus manifestaciones.
El estudio de la luz revela una serie de características y efectos al interactuar con la materia, que permiten desarrollar
algunas teorías sobre su naturaleza

TEORIA CORPUSCULAR
Supone que la luz está formada por partículas materiales, que llamó corpúsculos que son lanzados
gran velocidad por los cuerpos emisores de luz. Permite explicar fenómenos como
- La propagación rectilínea de la luz en el medio, ya que los focos luminosos emitirían minúsculas
partículas que se propagan en todas direcciones y que al chocar con nuestros ojos, producen la
sensación luminosa.
- La reflexión
- La refracción

Newton supuso que los corpúsculos eran muy pequeños en comparación con la materia y que
se propagan sin rozamiento por el medio. Teniendo en cuenta esto, los corpúsculos chocaban
elásticamente contra la superficie de separación entre dos medios. Como la diferencia de masas
es muy grande los corpúsculos rebotaban, de modo que la componente horizontal de la cantidad
de movimiento px se mantiene constante mientras que la componente normal py cambia de sentido.
Se cumplía la ley de la reflexión, el ángulo de incidencia y de reflexión eran iguales.
En la refracción, al pasar la luz de propagarse por aire a hacerlo por agua, los corpúsculos atraídos,
por el agua, eran acelerados al entrar en ella. Por tanto py aumentaba y los corpúsculos variaban su
dirección de propagación acercándose a la normal. Según esto, la velocidad de propagación de la luz
en agua es mayor que en el aire. ( como ya hemos visto por Huygens, ocurre lo contrario, si v´
disminuye se acerca a la normal). Esto podía permitir distinguir una y otra teoría.
Por ultimo también consideraba que los diferentes colores que formaban la luz blanca se deben a
diferentes tipos de corpúsculos, cada uno responsable de un color.
Con esta teoría no podían abordarse fenómenos como la difracción de la luz.

TEORIA ONDULATORIA
La luz es un fenómeno ondulatorio de tipo mecánico, como el sonido o las ondas en la superficie
del agua.
• Son ondas que se propagan en un medio.
En 1801 hace Thomas YOUNG (1773-1829) y En 1822 Augustin J. FRESNEL (1788-1872)
experimentos demostrando la interferencia de rayos de luz. Eso era un apoyo fuerte para la teoría,
ya que el modelo corpuscular era incapaz de explicar estos resultados.
• En 1864 MAXWELL plantea las ecuaciones del electromagnetismo y se ve que la luz es una onda
electromagnética (no una onda mecánica).
• Este punto fue confirmado experimentalmente por HERTZ en 1888 al producir y detectar ondas
electromagnéticas.
Teoría ondulatoría de Huygens
Huygens propuso que la luz consiste en la propagación de una perturbación ondulatoria del medio.
Creía que eran ondas longitudinales similares a las sonoras. Se sabía que la luz puede propagarse
en el vacío. Se inventa un medio muy sutil y de perfecta elasticidad que permita dicha propagación.
Se le llama éter.
Explicaba fácilmente fenómenos como reflexión y la refracción. Contra esta teoría se argumentaba
que si era una onda debía haber fenómenos de difracción e interferencia que no se habían encontrado
porque su longitud de onda es muy pequeña y que el resto lo explicaba la teoría corpuscular.

TEORIA ELECTROMACNETICA
Esta teoría considera que la luz es una onda electromagnética, consistente en un campo eléctrico
que varía en el tiempo generando a su vez un campo magnético y viceversa, ya que los campos
eléctricos variables generan campos magnéticos (ver ley de Ampère) y los campos magnéticos
variables generan campos eléctricos (ver ley de Faraday). De esta forma, la onda se autopropaga
indefinidamente a través del espacio, con campos magnéticos y eléctricos generándose continuamente.
Estas ondas electromagnéticas son sinusoidales, con los campos eléctrico y magnético perpendiculares
entre sí y respecto a la dirección de propagación.
Para poder describir una onda electromagnética podemos utilizar los parámetros habituales de cualquier onda:
* Amplitud (A): Es la longitud máxima respecto a la posición de equilibrio que alcanza la onda en su
desplazamiento.
* Periodo (T): Es el tiempo necesario para el paso de dos máximos o mínimos sucesivos por un punto fijo
en el espacio.
* Frecuencia (v): Número de oscilaciones del campo por unidad de tiempo. Es una cantidad inversa al periodo.
* Longitud de onda (λ): Es la distancia lineal entre dos puntos equivalentes de ondas sucesivas.
* Velocidad de propagación (V): Es la distancia que recorre la onda en una unidad de tiempo. En el caso de
la rapidez de propagación de la luz en el vacío, se representa con la letra c.

LA REFELXION DE LA LUZ
LEYES DE SNELL:
La ley de Snell es una fórmula utilizada para calcular el ángulo de refracción de la luz al
atravesar la superficie de separación entre dos medios de propagación de la luz (o cualquier
onda electromagnética) con índice de refracción distinto. El nombre proviene de su descubridor,
el matemático holandés Willebrord Snel van Royen (1580-1626). La denominaron "Snell" debido
a su apellido pero le pusieron dos "l" por su nombre Willebrord el cual lleva dos "l".
La misma afirma que la multiplicación del índice de refracción por el seno del ángulo de incidencia
es constante para cualquier rayo de luz incidiendo sobre la superficie separatriz de dos medios.
Aunque la ley de Snell fue formulada para explicar los fenómenos de refracción de la luz se puede
aplicar a todo tipo de ondas atravesando una superficie de separación entre dos medios en los que
la velocidad de propagación de la onda varíe.
SUPERFICIES REFLECTORAS:
Un reflector es una superficie que refleja la luz o cualquier otro tipo de onda.
En muchos casos, como el de las antenas parabólicas o algunos espejos concentradores de luz,
las superficies reflectoras tienen la forma de una parábola, o más precisamente de un paraboloide
de revolución; y por ello cumplen con su principal propiedad: que todos los haces que chocan en
ellas se reflejan en un punto en común, llamado foco.

REFLECTOR FOTOGRÁFICO
Puesto que la luz desempeña un rol tan importante en las tomas, los reflectores son uno de los
principales aliados de todo fotógrafo y muy especialmente a la hora de hacer sesiones de estudio,
una fotografía digamos más profesional.
Los efectos son muy buscados, ya que básicamente aumentan el contraste en las áreas iluminadas
y a la vez disminuyen las sombras molestas. La luz que rebota en un reflector puede utilizarse como
luz de relleno fácilmente (la ley inversa del cuadrado, y por lo tanto la distancia es determinante, tanto
como su tamaño). El manejo es sencillo, hay que tener sólo en cuenta que la luz que rebota en un
reflector regresa en el mismo ángulo en el que ésta incide sobre él. EJ: si la luz incide a 45º, es reflejada
a 45º.
Su uso, en múltiples ocasiones, evita la utilización del flash, pudiendo así lograr tomas con una iluminación
mucho menos forzada. Los reflectores están hechos con materiales especialmente eficaces, para que a la
hora de refractar la luz, sea el efecto buscado. Las unidades de flash sin reflectores, prácticamente no son
adecuadas para la fotografía profesional de estudio, porque al encontrarse en superficies reducidas, éstas
despiden una luz muy dura que puede ocasionar problemas de transición entre claros y oscuros. Su
utilización es totalmente válida en exteriores sin necesidad de focos y flashes, prevaleciendo la luz natural.
La rectificación de la fuente de luz se realiza mediante el uso de dichos reflectores que radian la luz en una
sola dirección. La forma de la luz a través del reflector puede comprimirse en un haz o dispersarse. Cuanto
más dispersa sea la luz, más suave será tu efecto. Los reflectores son una de las herramientas más útiles
para la macro-fotografía de flores e insectos.
TIPOS DE REFLECTORES Y EFECTOS
Blanco/Plateado
Por lo general, el más conocido es el reflector blanco. Lo que produce dicho reflector es una luz suave,
que lo hace ideal para rellenar algunas sombras en los retratos. Si colocamos al personaje u objeto a
fotografiar junto a una ventana, la luz entrará de lado, seguramente produciendo sombras bajo la nariz,
los ojos y la mandíbula (en el caso de un retrato), sobre todo si la luz es muy fuerte. Colocando entonces
un reflector (concretamente el blanco) en el lado opuesto a la ventana, éstas pueden atenuarse. También
tenemos el reflector plateado, que es el más refractante. Éste ayudará a compensar la falta de focos
cuando se requiere iluminación profesional, pudiendo cubrir el lugar de uno de ellos. Los reflectores blancos
son los favoritos de los fotógrafos. Los plateados, por lo general, reflejan demasiada luz. El reflector blanco
ofrece un resultado suave y con unos colores naturales. El reflector plateado es perfecto para una mayor
luminosidad. Acentúa indirectamente la luz y el contraste. No modifica el color.
Dorados
Los reflectores dorados tienden a darle un tono más acogedor a las fotografías, pues ofrecen un reflejo de
luz más caliente. Este tipo de luz hace que la piel adquiera un cierto brillo que la hace más atractiva. Este
reflector aporta un matiz cálido a la luz que refracta. Suele utilizarse en tomas al aire libre durante
primavera – verano, para acentuar los rasgos característicos de estas coloridas estaciones o incluso en
atardeceres. A la hora de hacer retratos o sesiones de estudio, a veces se emplea para darle a la piel
del modelo un sutil brillo, a fin de hacerla más tostada y mejor luminosidad.El reflector dorado, en sí mismo,
logra unos colores más cálidos.
Fuego Solar o Sunlight
Dentro de los de uso más específico, también tenemos los de fuego solar o sunlight, que poseen franjas
doradas y plateadas. Esta combinación refleja fuertemente la luz, pero dándole un toque cálido. Se puede
decir que pretende crear el efecto de luz solar, cuyas franjas plateadas son más anchas para reflejar mucha
más luz. Por lo general, éstos son muy utilizados en las fotografías de bodas. Reflejan una gran cantidad de
luz y a la vez tienen la ventaja del reflector dorado.
Reflector translúcido
La tela neutra translúcida reduce la intensidad de la luz en aproximadamente 1 f/stops, al tiempo que la atenúa
y distribuye. El reflector translúcido se utiliza para lograr una luz suave.
Negro
El reflector negro busca un efecto totalmente opuesto,elimina los reflejos absorbiendo la luz. Éste resulta
especialmente útil al fotografiar superficies de cristal o plástico. Normalmente están dispuestos a hacer la
inversión, que por lo general, vienen combinados (un tipo de reflector de un lado y otro tipo del otro) y que
no necesariamente deben ser difíciles de llevar o guardar, puesto que vienen en diferentes tamaños. El
reflector negro sirve para crear efectos dramáticos. Permite eliminar los reflejos luminosos y obtener efectos
con las sombras.
Otros reflectores más específicos:
Bounce card
El Bounce Card es un reflector más específico. De luz universal y orientable hasta el infinito, ofrece una
difusión inteligente de la luz que emite el flash o de las luces de estudio. Dicho reflector es polivalente y
plegable siendo compatible con todos los soportes de flash gracias a que poseen ,la inmensa mayoría,
un pie de fijación universal.
Beamer
Éste en concreto se utiliza para flash de largo alcance. Es un concentrador de la luz del flash para el uso
con teleobjetivos.

ESPEJOS PLANOS & ESFERICOS
ESPEJOS PLANOS:
Un espejo plano es una superficie plana muy pulimentada que puede reflejar la luz que le llega
con una capacidad reflectora de la intensidad de la luz incidente del 95% (o superior) .
Los espejos planos se utilizan con mucha frecuencia. Son los que usamos cada mañana
para mirarnos. En ellos vemos nuestro reflejo, una imagen que no está distorsionada.

ESPEJOS ESFERICOS:
Un espejo esférico está caracterizado por su radio de curvatura R. En el caso
de los espejos esféricos solo existe un punto focal F=F´=R/2 cuya posición
coincide con el punto medio entre el centro del espejo y el vértice del mismo.
Se encontrará a la izquierda del vértice para los espejos cóncavos y a la derecha
para los espejos convexos.
El aumento del espejo será A =y´/y y dependerá de la curvatura del espejo y de
la posición del objeto.
FORMACION DE OBJETOS:
La construcción de imágenes es muy sencilla si se utilizan los rayos principales:
- Rayo paralelo: Rayo paralelo al eje óptico que parte de la parte superior
- del objeto. Después de refractarse pasa por el foco imagen.
- Rayo focal: Rayo que parte de la parte superior del objeto y pasa por el foco
- objeto, con lo cual se refracta de manera que sale paralelo . Después de
- refractarse pasa por el foco imagen.
- Rayo radial: Rayo que parte de la parte superior del objeto y está dirigido
- hacia el centro de curvatura del dioptrio. Este rayo no se refracta y continúa
- en la mismas dirección ya que el ángulo de incidencia es igual a cero.
Hay que distinguir entre los espejos cóncavos y los convexos:
Espejos cóncavos:
 |
a) Objeto situado a la izquierda del centro de curvatura. La imagen es real, invertida y situada entre el centro y el foco. Su tamaño es menor que el objeto. |
| b) Objeto situado en el centro de curvatura. La imagen es real, invertida y situada en el mismo punto. Su tamaño igual que el objeto. | |
| c) Objeto situado entre el centro de curvatura y el foco. La imagen es real, invertida y situada a la izquierda del centro de curvatura. Su tamaño es mayor que el objeto. | |
| d) Objeto situado en el foco del espejo. Los rayos reflejados son paralelos y la imagen se forma en el infinito. | |
| e) Objeto situado a la derecha del foco. La imagen es virtual, y conserva su orientación. Su tamaño es mayor que el objeto. |
Espejos convexos:
Se produce una situación en la que la imagen es virtual, derecha y más pequeña que el objeto.
|
Se produce una situación en la que la imagen es virtual, derecha y más pequeña que el objeto. |
|
Para observar la formación de rayos pulsa start y cambia la posición del objeto y el radio de curvatura
de los espejos. Se puede cambiar entre lentes y espejos.
Imagenes reales e Imagenes virtuales
|
Normalmente cada punto de un objeto emite luz en muchas direcciones. Para simplificar nuestros dibujos nosotros dibujaremos dos o tres rayos. Estos rayos de luz son desviados al pasar por lentes o al chocar con espejos.
Si la luz que procede de un objeto después de sufrir cambios de dirección se junta en un punto del espacio diremos que allí existe una imagen real del objeto. Una pantalla, una atmósfera con humo, un negativo fotográfico colocados en ese punto recogerán la luz que proviene del objeto y veremos una imagen modificada de él. Si la luz que proviene de cada punto del objeto no se junta en un punto sino en una zona del espacio entonces la imagen será borrosa. A cada punto del objeto le corresponderá una zona y la imagen no se verá nítida. Si la luz que procede de un objeto no se junta sino que se separa cada vez más no se forma una imagen. Las pantallas no recogerán una imagen en absoluto. Pero si colocamos nuestros ojos en la dirección correcta, veremos estos rayos separándose. Puede ocurrir que para nuestros ojos parezca que provienen de un punto. En ese punto nuestro ojo va a construir una imagen. Se llama imagen virtual.Es una construcción mental a partir de rayos que se separan.
También los espejismos son imágenes virtuales como bien saben los viajeros perdidos por el desierto. Los Bahr el Shaitan o Lagos de Satán –nombre con el que los árabes designan a los espejismos de agua en el desierto-, así como los “charcos” que aparecen en la cinta asfáltica, son imágenes refractadas del cielo; asimismo, las islas que se supone existen en el mar son resultado de la refracción de montañas, barcos y ciudades que, casi siempre, se encuentran a muchos kilómetros de distancia |
LA REFRACCION DE LA LUZ
Se denomina refracción luminosa al cambio que experimenta la dirección de propagación de la luz cuando atraviesa oblicuamente la superficie de separación de dos medios transparentes de distinta naturaleza. Las lentes, las máquinas fotográficas, el ojo humano y, en general, la mayor parte de los instrumentos ópticos basan su funcionamiento en este fenómeno óptico.
El fenómeno de la refracción va, en general, acompañado de una reflexión, más o menos débil, producida en la superficie que limita los dos medios transparentes. El haz, al llegar a esa superficie límite, en parte se refleja y en parte se refracta, lo cual implica que los haces reflejado y refractado tendrán menos intensidad luminosa que el rayo incidente. Dicho reparto de intensidad se produce en una proporción que depende de las características de los medios en contacto y del ángulo de incidencia respecto de la superficie límite. A pesar de esta circunstancia, es posible fijar la atención únicamente en el fenómeno de la refracción para analizar sus características.
Las leyes de la refracción
Al igual que las leyes de la reflexión, las de la refracción poseen un fundamento experimental. Junto con los conceptos de rayo incidente, normal y ángulo de incidencia, es necesario considerar ahora el rayo refractado y el ángulo de refracción o ángulo que forma la normal y el rayo refractado.
Sean 1 y 2 dos medios transparentes en contacto que son atravesados por un rayo luminoso en el sentido de 1 a 2 y e1 y e2 los ángulos de incidencia y refracción respectivamente. Las leyes que rigen el fenómeno de la refracción pueden, entonces, expresarse en la forma:
1.ª Ley. El rayo incidente, la normal y el rayo refractado se encuentran en el mismo plano.
2.ª Ley. (ley de Snell) Los senos de los ángulos de incidencia e1 y de refracción e2 son directamente proporcionales a las velocidades de propagación v1 y v2 de la luz en los respectivos medios.
![]()
Recordando que índice de refracción y velocidad son inversamente proporcionales la segunda ley de la refracción se puede escribir en función de los índices de refracción en la forma:
![]()
o en otros términos:
n1 · sen e1 = n2 · sen e2 = cte
Esto indica que el producto del seno del ángulo e por el índice de refracción del medio correspondiente es una cantidad constante y, por tanto, los valores de n y sen e para un mismo medio son inversamente proporcionales.
Debido a que la función trigonométrica seno es creciente para ángulos menores de 90º, de la última ecuación se deduce que si el índice de refracción ni del primer medio es mayor que el del segundo n2, el ángulo de refracción e2 es mayor que el de incidencia e1 y, por tanto, el rayo refractado se aleja de la normal.
Por el contrario, si el índice de refracción n1 del primer medio es menor que el del segundo n2, el ángulo de refracción e2 es menor que el de incidencia el y el rayo refractado se acerca a la normal.
Estas reglas prácticas que se deducen de la ecuación son de mucha utilidad en la representación de la marcha de los rayos, operación imprescindible en el estudio de cualquier fenómeno óptico desde la perspectiva de la óptica geométrica.
La refringencia de un medio transparente viene medida por su índice de refracción. Los medios más refringentes son aquellos en los que la luz se propaga a menor velocidad; se dice también que tienen una mayor densidad óptica. Por regla general, la refringencia de un medio va ligada a su densidad de materia, pues la luz encontrará más dificultades para propagarse cuanta mayor cantidad de materia haya de atravesar para una misma distancia. Así pues, a mayor densidad, menor velocidad y mayor índice de refracción o grado de refringencia.
Lentes Convergentes
1. Un rayo paralelo
Pasa por el foco del lado de la imagen de una lente convergente

2. Un rayo central o rayo principal es el que pasa por el centro dellente y no se desvía.

3. Un rayo focal
Pasa por el foco del lado del objeto en una lente convergente, y después
de atravesarla, es paralelo al eje óptico de ella


Acción de una sección delente convergente sobre un haz de rayos paralelos.

Laslentes convergentes pueden formar imágenes virtuales mayores que el objeto
(Lupa).

Lentes Divergentes
1. Rayo Paralelo parece emanar del foco, del lado del objeto, en el ladodel objeto de una lente divergente
2. Un rayo central o rayo principal es el que pasa por el centro dellente y no se desvía.
3. Un rayo focal es paralelo al eje óptico de una lente divergente y despuésde atravesarla parece provenir del foco del lado del objeto en una lentedivergente.

Acción de una sección delente divergente sobre un haz de rayos paralelos.

Laslentes divergentes siempre forman imágenes virtuales menores que el objeto.

CARACTERISTICAS FORMADAS DADAS POR UNA LENTE
Notación
- EO = Elemento óptico.
- EOP = Elemento Óptico Primario u Objetivo (lente, espejo, prisma); es el que recolecta la luz.
- EOS = Elemento Óptico Secundario (espejo, lente, prisma secundario)
Características
- Brillantez aparente: depende directamente del área recolectora de luz. Entre más grande dicha área más brillante será la imagen.
- Contraste: es la diferencia que se nota entre distintos colores o entre las distintas tonalidades de un mismo color. A mayor contraste mayor nitidez en la imagen.
- Refracción: desviación de la luz cuando ésta atraviesa un medio diferente de aquel en el cual se estaba propagando. Ejemplo: cuando la luz proviene del espacio y entra en el “medio” atmosférico terrestre, la luz se desvía; cuando la luz pasa del aire al vidrio, se desvía o refracta, y viceversa.
- Plano Focal [PFoc] , Pto. Focal [PF] y Longitud Focal [LF]: si se sitúa un objeto muy lejos (o a una distancia “infinita“, en lenguaje coloquial) del elemento óptico, los rayos provenientes del objeto llegarán paralelos al eje óptico, y al formarse su imágen, tanto por reflexión (espejo) como por refracción (lente), la misma estará situada “espacialmente” en un plano imaginario llamado PFoc, es decir, todos los rayos luminosos provenientes del objeto lejano deben converger (cada uno) a un Pto. Focal o Fococorrespondiente, para que la imagen del objeto esté bien definida (fig.No. 19). Así, la imagen del objeto lejano no es más que la suma o integración de todos los ptos. focales formados por todos los rayos luminosos que provienen del objeto, y el lugar “espacial o geométrico” de cada uno de tales focos se encuentra en un plano ficticio (el PFoc)… El objeto en el “infinito” se usa solamente para determinar/definir el PF del elemento óptico. Cuando el objeto se encuentra cerca del elemento óptico, su imágen no se formará en el PFoc, sino que se formará en el llamado Plano Imágen, PI (fig.No. 20). De la misma forma, el PI no es más que la suma de todos los rayos provenientes del objeto cercano, los cuales pasan por el PF del elemento óptico, y convergen en el PI. La Longitud Focal no es más que la distancia entre el centro óptico del espejo o lente (delgada) y el PFoc.
Defectos (aberraciones) inherentes a las lentes y espejos
Estos defectos son propios de los RFRs y de los oculares. Dichos defectos producen imágenes con colores falsos (entre más grande la lente, más sufre de estos defectos): para corregir estos defectos se construyen lentes con diferentes tipos de vidrio, con diferentes geometrías y diferente contenido químico y se los agrupa en conjuntos de varios EOs para que así los defectos de unos se compensen con la geometría y posición de otros, como veremos en la sección de oculares. También se les recubre de un material adecuado para tratar de disminuir tales defectos.
- Aberración esférica [AE]: Los rayos de luz convergen en diferentes lugares o puntos focales y no en un solo PFoc, produciendo imágenes poco definidas (no puntuales y difusas). Esto es causado por la geometría del EO.
INSTRUMENTOS OPTICOS
Un instrumento óptico sirve para procesar ondas de luz con el fin de mejorar una imagen para su visualización, y para analizar las ondas de luz (o fotones) para determinar propiedades características.
ORIGENES & USOS:
Los primeros instrumentos ópticos fueron telescopios utilizados para la magnificación de imágenes (distantes), y microscopiosutilizados para magnificar imágenes muy pequeñas. Desde los días de Galileo y van Leeuwenhoek, estos instrumentos han sido mejorados ampliamente y se han extendido a otras porciones del espectro electromagnético.
ANALISIS:
Otra clase de instrumentos ópticos es utilizada para analizar las propiedades de la luz o de materiales ópticos. Entre ellos se incluyen:
- Interferómetro para medir la interferencia de las ondas de luz.
- Fotómetro para medir la intensidad de la luz.
- Polarímetro para medir la dispersión o rotación de luz polarizada.
- Reflectómetro para medir la reflectividad de la superficie de un objeto.
- Refractómetro para medir índice de refracción de varios materiales, inventado por Ernst Abbe.
EL MICROSCOPIO:
s un instrumento que permite observar objetos que son demasiado pequeños para ser vistos a simple vista. El tipo más común y el primero que se inventó es el microscopio óptico. Se trata de un instrumento óptico que contiene dos o más lentes que permiten obtener una imagen aumentada del objeto y que funciona por refracción. La ciencia que investiga los objetos pequeños utilizando este instrumento se llama microscopía.
El microscopio fue inventado por Zacharias Janssen en 1590. En 1665 aparece en la obra de William Harvey sobre la circulación sanguínea al mirar al microscopio los capilares sanguíneos y Robert Hooke publica su obra Micrographia.

CAMARA FOTOGRAFICA:
Una cámara fotográfica o cámara de fotos es un dispositivo utilizado para capturar imágenes o fotografías. Es un mecanismo antiguo para proyectar imágenes, en el que una habitación entera desempeñaba las mismas funciones que una cámara fotográfica actual por dentro, con la diferencia que en aquella época no había posibilidad de guardar la imagen a menos que ésta se trazara manualmente. Las cámaras actuales pueden ser sensibles al espectro visible o a otras porciones del espectro electromagnético y su uso principal es capturar la imagen que se encuentra en el campo visual.
Las cámaras fotográficas constan de una cámara oscura cerrada, con una abertura en uno de los extremos para que pueda entrar la luz, y una superficie plana de formación de la imagen o de visualización para capturar la luz en el otro extremo. La mayoría de las cámaras fotográficas tienen un objetivo formado de lentes, ubicado delante de la abertura de la cámara fotográfica para controlar la luz entrante y para enfocar la imagen, o parte de la imagen. El diámetro de esta abertura (conocido como apertura) suele modificarse con un diafragma, aunque algunos objetivos tienen apertura fija.
Mientras que la apertura y el brillo de la escena controlan la cantidad de luz que entra por unidad de tiempo, en la cámara durante el proceso fotográfico, el obturador controla el lapso en que la luz incide en la superficie de grabación. Por ejemplo, en situaciones con poca luz, la velocidad de obturación será menor (mayor tiempo abierto) para permitir que la película reciba la cantidad de luz necesaria para asegurar una exposición correcta.

CUARTO PERIODO
ELECTRCIDAD & MAGNETISMO
La electricidad y el magnetismo están estrechamente relacionados y son temas de gran importancia en la física. Usamos electricidad para suministrar energía a las computadoras y para hacer que los motores funcionen. El magnetismo hace que un compás o brújula apunte hacia el norte, y hace que nuestras notas queden pegadas al refrigerador. Sin radiación electromagnética viviríamos en la obscuridad ¡pues la luz es una de sus muchas manifestaciones.

Líneas de campo magnético alrededor de dos imanes de barra.
La electricidad puede existir como carga estacionaria, conocida como electricidad estática; también puede estar en movimiento y fluyendo, conocida como corriente eléctrica. Las partículas subatómicas tales como los protones y electrones, poseen cargas eléctricas minúsculas. En tiempos relativamente recientes, la humanidad ha aprendido a almacenar el poder de la electricidad. Este poder, y los muchos tipos de circuitos y dispositivos eléctricos que el hombre ha inventado, han transformado el mundo de manera radical. La electricidad también juega un papel importante en el mundo natural, cuando se generan poderosos rayos que producen señales que se desplazan a través de nuestros nervios.
El magnetismo es primo hermano de la electricidad. Algunos materiales, tales como el hierro, son atraídos por imanes, mientras que otros, como el cobre, ignoran su influencia. Describimos el movimiento de objetos influenciados por imánes en términos de campos magnéticos. Sabemos que los imanes tienen polo norte y polo sur, y que polos iguales se rechazan entre sí, mientras que polos opuestos se atraen. La electricidad y el magnetismo son dos caras de una simple fuerza fundamental. Al acelerar un imán se producirá una corriente eléctrica, si varías el flujo de electricidad, se origina un campo magnético. Estos principios los usamos en la construcción de motores y generadores.
INDUCCION ELECTROSTATICA.
La inducción electrostática es la redistribución de la carga eléctrica en un objeto, causada por la influencia de cargas cercanas. La inducción fue descubierta por el científico británico John Canton en 1753, y por el profesor sueco Johan Carl Wilcke en 1762. Los generadores electrostáticos como la máquina de Wimshurst, el generador de Van de Graaff o el electróforo se valen de este principio. La inducción electrostática no debe confundirse con la inducción electromagnética aunque normalmente ambas se conocen como «inducción».

Demostración de inducción en 1870. El terminal positivo de una máquina electrostática se sitúa cerca del cilindro de latón, consiguiendo que la parte izquierda adquiera una carga positiva, y la parte derecha una carga negativa. Los pequeños electroscopios de bola que cuelgan de la parte inferior muestran que la carga se concentra en los extremos.
EXPLICACION
Una pieza normal de materia tiene el mismo número de cargas eléctricas positivas y negativas en cada una de sus partes, situadas muy cerca unas de otras, por lo que en general se considera que no tienen carga, o que su carga eléctrica acumulada es cero. Cuando un objeto con carga se acerca a un objeto sin carga capaz de conducir la electricidad, como una pieza de metal, la fuerza que ejerce la carga cercana hace que las cargas se separen. Por ejemplo, si se lleva una carga positiva cerca del objeto (ver imagen de la derecha), las cargas negativas del metal serán atraídas hacía él, y se desplazarán hacía el objeto hasta ponerse frente a él, mientras las cargas positivas serán repelidas y se desplazarán hacía el punto más alejado del objeto. Esto trae como consecuencia una zona de cargas negativas sobre el objeto más cercano a las cargas externas, y una zona de cargas positivas en el punto más lejano a él. Si la carga externa es negativa, la polaridad de las regiones con carga eléctrica se invertirá. Al tratarse únicamente de una redistribución de las cargas, el objeto no tiene en sí carga eléctrica de ningún tipo. Este efecto inductivo es reversible; si se suprime la carga cercana, la atracción entre las cargas internas positivas y negativas hará que éstas se entremezclen de nuevo.
Una corrección de poca importancia respecto a la imagen superior es que sólo las cargas negativas de la materia, es decir los electronesson libres para moverse, las cargas positivas, los átomos del núcleo están unidos a la estructura de la materia sólida. Por lo tanto, todo el movimiento de las cargas, es el resultado del movimiento únicamente de los electrones. En el ejemplo de arriba, los electrones se desplazan de la parte izquierda del objeto a la parte derecha. Sin embargo, cuando un número de electrones sale de una zona, dejan una carga positiva desequilibrada debido al núcleo. Así pues, el movimiento de los electrones crea tanto la región cargada positivamente como la cargada negativamente que se describen arriba.
LEY DE COULOMB
La ley de Coulomb puede expresarse como:
- La magnitud de cada una de las fuerzas eléctricas con que interactúan dos cargas puntuales en reposo es directamente proporcional al producto de la magnitud de ambas cargas e inversamente proporcional al cuadrado de la distancia que las separa y tiene la dirección de la línea que las une. La fuerza es de repulsión si las cargas son de igual signo, y de atracción si son de signo contrario.
La constante de proporcionalidad depende de la constante dieléctrica del medio en el que se encuentran las cargas.

Ley de Coulomb expresando los signos de cargas de diferente signo, y de carga del mismo signo.
Desarrollo de la ley
Charles-Augustin de Coulomb desarrolló la balanza de torsión con la que determinó las propiedades de la fuerza electrostática. Este instrumento consiste en una barra que cuelga de una fibra capaz de torcerse. Si la barra gira, la fibra tiende a hacerla regresar a su posición original, con lo que conociendo la fuerza de torsión que la fibra ejerce sobre la barra, se puede determinar la fuerza ejercida en un punto de la barra. La ley de Coulomb también conocida como ley de cargas tiene que ver con las cargas eléctricas de un material, es decir, depende de si sus cargas son negativas o positivas.
En la barra de la balanza, Coulomb colocó una pequeña esfera cargada y a continuación, a diferentes distancias, posicionó otra esfera también cargada. Luego midió la fuerza entre ellas observando el ángulo que giraba la barra.
Dichas mediciones permitieron determinar que:
- La fuerza de interacción entre dos cargas
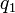 y
y  duplica su magnitud si alguna de las cargas dobla su valor, la triplica si alguna de las cargas aumenta su valor en un factor de tres, y así sucesivamente. Concluyó entonces que el valor de la fuerza era proporcional al producto de las cargas:
duplica su magnitud si alguna de las cargas dobla su valor, la triplica si alguna de las cargas aumenta su valor en un factor de tres, y así sucesivamente. Concluyó entonces que el valor de la fuerza era proporcional al producto de las cargas:


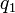 y
y 


en consecuencia:


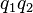
- Si la distancia entre las cargas es
 , al duplicarla, la fuerza de interacción disminuye en un factor de 4 (2²); al triplicarla, disminuye en un factor de 9 (3²) y al cuadriplicar
, al duplicarla, la fuerza de interacción disminuye en un factor de 4 (2²); al triplicarla, disminuye en un factor de 9 (3²) y al cuadriplicar  , la fuerza entre cargas disminuye en un factor de 16 (4²). En consecuencia, la fuerza de interacción entre dos cargas puntuales, es inversamente proporcional al cuadrado de la distancia:
, la fuerza entre cargas disminuye en un factor de 16 (4²). En consecuencia, la fuerza de interacción entre dos cargas puntuales, es inversamente proporcional al cuadrado de la distancia:


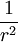
Asociando ambas relaciones:



Finalmente, se introduce una constante de proporcionalidad para transformar la relación anterior en una igualdad:
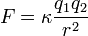
Enunciado de la ley
La ley de Coulomb es válida sólo en condiciones estacionarias, es decir, cuando no hay movimiento de las cargas o, como aproximación cuando el movimiento se realiza a velocidades bajas y en trayectorias rectilíneas uniformes. Es por ello que es llamada fuerza electrostática.
En términos matemáticos, la magnitud  de la fuerza que cada una de las dos cargas puntuales
de la fuerza que cada una de las dos cargas puntuales 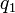 y
y  ejerce sobre la otra separadas por una distancia
ejerce sobre la otra separadas por una distancia  se expresa como:
se expresa como:
Dadas dos cargas puntuales 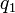 y
y  separadas una distancia
separadas una distancia  en el vacío, se atraen o repelen entre sí con una fuerza cuya magnitud está dada por:
en el vacío, se atraen o repelen entre sí con una fuerza cuya magnitud está dada por:
La Ley de Coulomb se expresa mejor con magnitudes vectoriales:
donde 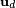 es un vector unitario, siendo su dirección desde la cargas que produce la fuerza hacia la carga que la experimenta.
es un vector unitario, siendo su dirección desde la cargas que produce la fuerza hacia la carga que la experimenta.
Al aplicar esta fórmula en un ejercicio, se debe colocar el signo de las cargas q1 o q2, según sean éstas positivas o negativas.
El exponente (de la distancia: d) de la Ley de Coulomb es, hasta donde se sabe hoy en día, exactamente 2. Experimentalmente se sabe que, si el exponente fuera de la forma 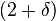 , entonces
, entonces 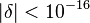 .
.
Obsérvese que esto satisface la tercera de la ley de Newton debido a que implica que fuerzas de igual magnitud actúan sobre 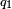 y
y  . La ley de Coulomb es una ecuación vectorial e incluye el hecho de que la fuerza actúa a lo largo de la línea de unión entre las cargas.
. La ley de Coulomb es una ecuación vectorial e incluye el hecho de que la fuerza actúa a lo largo de la línea de unión entre las cargas.
Constante de Coulomb
La constante 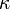 es la Constante de Coulomb y su valor para unidades SI es
es la Constante de Coulomb y su valor para unidades SI es 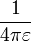 Nm²/C².
Nm²/C².
A su vez la constante  donde
donde 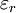 es la permitividad relativa,
es la permitividad relativa,  , y
, y 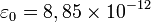 F/m es la permitividad del medio en el vacío.
F/m es la permitividad del medio en el vacío.
Cuando el medio que rodea a las cargas no es el vacío hay que tener en cuenta la constante dieléctrica y la permitividad del material.
La ecuación de la ley de Coulomb queda finalmente expresada de la siguiente manera:
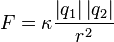 |
|---|
La constante, si las unidades de las cargas se encuentran en Coulomb es la siguiente  y su resultado será en sistema MKS (
y su resultado será en sistema MKS ( ). En cambio, si la unidad de las cargas están en UES (q), la constante se expresa de la siguiente forma
). En cambio, si la unidad de las cargas están en UES (q), la constante se expresa de la siguiente forma  y su resultado estará en las unidades CGS (
y su resultado estará en las unidades CGS ( ).
).
Potencial de Coulomb
La ley de Coulomb establece que la presencia de una carga puntual general induce en todo el espacio la aparición de un campo de fuerzas que decae según la ley de la inversa del cuadrado. Para modelizar el campo debido a varias cargas eléctricas puntuales estáticas puede usarse el principio de superposición dada la aditividad de las fuerzas sobre una partícula. Sin embargo, matemáticamente el manejo de expresiones vectoriales de ese tipo puede llegar a ser complicado, por lo que frecuentemente resulta más sencillo definir un potencial eléctrico. Para ello a una carga puntual 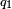 se le asigna una función escalar o potencial de Coulomb
se le asigna una función escalar o potencial de Coulomb  tal que la fuerza dada por la ley de Coulomb sea expresable como:
tal que la fuerza dada por la ley de Coulomb sea expresable como:
De la ley de Coulomb se deduce que la función escalar que satisface la anterior ecuación es:
Donde:
-
 , es el vector posición genérico de un punto donde se pretende definir el potencial de Coulomb y
, es el vector posición genérico de un punto donde se pretende definir el potencial de Coulomb y
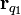 , es el vector de posición de la carga eléctrica
, es el vector de posición de la carga eléctrica  cuyo campo pretende caracterizarse por medio del potencial.
cuyo campo pretende caracterizarse por medio del potencial.
Limitaciones de la Ley de Coulomb
- La expresión matemática solo es aplicable a cargas puntuales estacionarias, y para casos estáticos más complicados de carga necesita ser generalizada mediante el potencial eléctrico.
- Cuando las cargas eléctricas están en movimiento es necesario reemplazar incluso el potencial de Coulomb por el potencial vector de Liénard-Wiechert, especialmente si las velocidades de las partículas son grandes comparadas con la velocidad de la luz.
Verificación experimental de la Ley de Coulomb
Es posible verificar la ley de Coulomb mediante un experimento sencillo. Considérense dos pequeñas esferas de masa "m" cargadas con cargas iguales, del mismo signo, y que cuelgan de dos hilos de longitud l, tal como se indica en la figura adjunta. Sobre cada esfera actúan tres fuerzas: el peso mg, la tensión de la cuerda T y la fuerza de repulsión eléctrica entre las bolitas 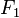 . En el equilibrio:
. En el equilibrio:
(1)
y también:
(2)
Dividiendo () entre () miembro a miembro, se obtiene:
Siendo 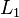 la separación de equilibrio entre las esferas cargadas, la fuerza
la separación de equilibrio entre las esferas cargadas, la fuerza 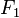 de repulsión entre ellas, vale, de acuerdo con la ley de Coulomb
de repulsión entre ellas, vale, de acuerdo con la ley de Coulomb  y, por lo tanto, se cumple la siguiente igualdad:
y, por lo tanto, se cumple la siguiente igualdad:
(3)
Al descargar una de las esferas y ponerla, a continuación, en contacto con la esfera cargada, cada una de ellas adquiere una carga q/2, en el equilibrio su separación será  y la fuerza de repulsíón entre las mismas estará dada por:
y la fuerza de repulsíón entre las mismas estará dada por:
Por estar en equilibrio, tal como se dedujo más arriba:  . Y de modo similar se obtiene:
. Y de modo similar se obtiene:
(4)
Dividiendo () entre (), miembro a miembro, se llega a la siguiente igualdad:
(5)
Midiendo los ángulos 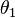 y
y  y las separaciones entre las cargas
y las separaciones entre las cargas 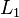 y
y 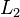 es posible verificar que la igualdad se cumple dentro del error experimental. En la práctica, los ángulos pueden resultar difíciles de medir, así que si la longitud de los hilos que sostienen las esferas son lo suficientemente largos, los ángulos resultarán lo bastante pequeños como para hacer la siguiente aproximación:
es posible verificar que la igualdad se cumple dentro del error experimental. En la práctica, los ángulos pueden resultar difíciles de medir, así que si la longitud de los hilos que sostienen las esferas son lo suficientemente largos, los ángulos resultarán lo bastante pequeños como para hacer la siguiente aproximación:
Con esta aproximación, la relación () se transforma en otra mucho más simple:
De esta forma, la verificación se reduce a medir la separación entre cargas y comprobar que su cociente se aproxima al valor indicado.
DIFERENCIA DE PONTENCIAL ELECTRICO
El potencial eléctrico o potencial electrostático en un punto, es el trabajo que debe realizar un campo electrostático para mover una carga positiva q desde dicho punto hasta el punto de referencia,1 dividido por unidad de carga de prueba. Dicho de otra forma, es el trabajo que debe realizar una fuerza externa para traer una carga positiva unitaria q desde el punto de referencia hasta el punto considerado en contra de la fuerza eléctrica. Matemáticamente se expresa por:
El potencial eléctrico sólo se puede definir para un campo estático producido por cargas que ocupan una región finita del espacio. Para cargas en movimiento debe recurrirse a los potenciales de Liénard-Wiechert para representar un campo electromagnético que además incorpore el efecto de retardo, ya que las perturbaciones del campo eléctrico no se pueden propagar más rápido que lavelocidad de la luz. Si se considera que las cargas están fuera de dicho campo, la carga no cuenta con energía y el potencial eléctrico equivale al trabajo necesario para llevar la carga desde el exterior del campo hasta el punto considerado. La unidad del Sistema Internacional es el voltio (V). Todos los puntos de un campo eléctrico que tienen el mismo potencial forman una superficie equipotencial. Una forma alternativa de ver al potencial eléctrico es que a diferencia de la energía potencial eléctrica o electrostática, él caracteriza sólo una región del espacio sin tomar en cuenta la carga que se coloca allí.
Trabajo eléctrico y energía potencial eléctrica
Considérese una carga electrica puntual  en presencia de un campo eléctrico
en presencia de un campo eléctrico  . La carga experimentará una fuerza eléctrica:
. La carga experimentará una fuerza eléctrica:
(1)
Esta fuerza realizará un trabajo para trasladar la carga de un punto A a otro B, de tal forma que para producir un pequeño desplazamiento 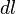 la fuerza eléctrica hará un trabajo diferencial
la fuerza eléctrica hará un trabajo diferencial  expresado como:
expresado como:
(2)
Por lo tanto, integrando la expresión () se obtiene el trabajo total realizado por el campo eléctrico:
(3)
Un caso particular de la fórmula anterior, es el de un campo eléctrico definido creado por una carga puntual estática Q. Sea una carga puntual  que recorre una determinada trayectoria A - B en las inmediaciones de una carga
que recorre una determinada trayectoria A - B en las inmediaciones de una carga  tal y como muestra la figura 1. Siendo
tal y como muestra la figura 1. Siendo  el desplazamiento infinitesimal de la carga
el desplazamiento infinitesimal de la carga  en la dirección radial, el trabajo diferencial
en la dirección radial, el trabajo diferencial  se puede expresar así:
se puede expresar así:
(4)
Para calcular el trabajo total, se integra entre la posición inicial A, distante 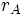 de la carga
de la carga  y la posición final B, distante
y la posición final B, distante  de la carga
de la carga  :
:
(5)
De la expresión () se concluye que el trabajo  no depende de la trayectoria seguida por la partícula, sólo depende de la posición inicial y final, lo cual implica que la fuerza eléctrica
no depende de la trayectoria seguida por la partícula, sólo depende de la posición inicial y final, lo cual implica que la fuerza eléctrica  es una fuerza conservativa. Por lo tanto se puede definir una energía potencial que permite calcular el trabajo más fácilmente:
es una fuerza conservativa. Por lo tanto se puede definir una energía potencial que permite calcular el trabajo más fácilmente:
(6)
El trabajo realizado por la fuerza eléctrica para desplazar una partícula entre A y B será:
(7)
Por convención, el nivel cero de energía potencial se suele establecer en el infinito, es decir, si y sólo si  .
.
Diferencia de potencial eléctrico
Considérese una carga de prueba positiva  en presencia de un campo eléctrico y que se traslada desde el punto A al punto B conservándose siempre en equilibrio. Si se mide el trabajo que debe hacer el agente que mueve la carga, la diferencia de potencial eléctrico se define como:
en presencia de un campo eléctrico y que se traslada desde el punto A al punto B conservándose siempre en equilibrio. Si se mide el trabajo que debe hacer el agente que mueve la carga, la diferencia de potencial eléctrico se define como:
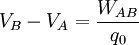
El trabajo 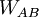 puede ser positivo, negativo o nulo. En estos casos el potencial eléctrico en B será respectivamente mayor, menor o igual que el potencial eléctrico en A. La unidad en el SI para la diferencia de potencial que se deduce de la ecuación anterior es Joule/Coulomb y se representa mediante una nueva unidad, el voltio, esto es: 1 voltio = 1 joule/coulomb.
puede ser positivo, negativo o nulo. En estos casos el potencial eléctrico en B será respectivamente mayor, menor o igual que el potencial eléctrico en A. La unidad en el SI para la diferencia de potencial que se deduce de la ecuación anterior es Joule/Coulomb y se representa mediante una nueva unidad, el voltio, esto es: 1 voltio = 1 joule/coulomb.
Un electronvoltio (eV) es la energía adquirida para un electrón al moverse a través de una diferencia de potencial de 1 V, 1 eV = 1,6x10-19 J. Algunas veces se necesitan unidades mayores de energía, y se usan los kiloelectronvoltios (keV), megaelectronvoltios (MeV) y los gigaelectronvoltios (GeV). (1 keV=103 eV, 1 MeV = 106 eV, y 1 GeV = 109 eV).
Aplicando esta definición a la teoría de circuitos y desde un punto de vista más intuitivo, se puede decir que el potencial eléctrico en un punto de un circuito representa la energía que posee cada unidad de carga al paso por dicho punto. Así, si dicha unidad de carga recorre un circuito constituyendóse en corriente eléctrica, ésta irá perdiendo su energía (potencial o voltaje) a medida que atraviesa los diferentes componentes del mismo. Obviamente, la energía perdida por cada unidad de carga se manifestará como trabajo realizado en dicho circuito (calentamiento en una resistencia, luz en una lámpara, movimiento en un motor, etc.). Por el contrario, esta energía perdida se recupera al paso por fuentes generadoras de tensión. Es conveniente distinguir entre potencial eléctrico en un punto (energía por unidad de carga situada en ese punto) y corriente eléctrica (número de cargas que atraviesan dicho punto por segundo).
Usualmente se escoge el punto A a una gran distancia (en rigor el infinito) de toda carga y el potencial eléctrico  a esta distancia infinita recibe arbitrariamente el valor cero. Esto permite definir el potencial eléctrico en un punto poniendo
a esta distancia infinita recibe arbitrariamente el valor cero. Esto permite definir el potencial eléctrico en un punto poniendo 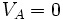 y eliminando los índices:
y eliminando los índices:
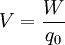
siendo 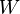 el trabajo que debe hacer un agente exterior para mover la carga de prueba
el trabajo que debe hacer un agente exterior para mover la carga de prueba  desde el infinito al punto en cuestión.
desde el infinito al punto en cuestión.
Obsérvese que la igualdad planteada depende de que se da arbitrariamente el valor cero al potencial  en la posición de referencia (el infinito) el cual hubiera podido escogerse de cualquier otro valor así como también se hubiera podido seleccionar cualquier otro punto de referencia.
en la posición de referencia (el infinito) el cual hubiera podido escogerse de cualquier otro valor así como también se hubiera podido seleccionar cualquier otro punto de referencia.
También es de hacer notar que según la expresión que define el potencial eléctrico en un punto, el potencial en un punto cercano a una carga positiva aislada es positivo porque debe hacerse trabajo positivo mediante un agente exterior para llevar al punto una carga de prueba (positiva) desde el infinito. Similarmente, el potencial cerca de una carga negativa aislada es negativo porque un agente exterior debe ejercer una fuerza (trabajo negativo en este caso) para sostener a la carga de prueba (positiva) cuando esta (la carga positiva) viene desde el infinito.
Por último, el potencial eléctrico queda definido como un escalar porque 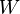 y
y  son escalares.
son escalares.
Tanto 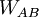 como
como 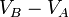 son independientes de la trayectoria que se siga al mover la carga de prueba desde el punto A hasta el punto B. Si no fuera así, el punto B no tendría un potencial eléctrico único con respecto al punto A y el concepto de potencial sería de utilidad restringida.
son independientes de la trayectoria que se siga al mover la carga de prueba desde el punto A hasta el punto B. Si no fuera así, el punto B no tendría un potencial eléctrico único con respecto al punto A y el concepto de potencial sería de utilidad restringida.
Es posible demostrar que las diferencias de potencial son independientes de la trayectoria para el caso especial representado en la figura. Para mayor simplicidad se han escogido los puntos A y B en una recta radial.
Una carga de prueba puede trasladarse desde A hacia B siguiendo la trayectoria I sobre una recta radial o la trayectoria II completamente arbitraria.
La trayectoria II puede considerarse equivalente a una trayectoria quebrada formada por secciones de arco y secciones radiales alternadas. Puesto que estas secciones se pueden hacer tan pequeñas como se desee, la trayectoria quebrada puede aproximarse a la trayectoria II tanto como se quiera. En la trayectoria II el agente externo hace trabajo solamente a lo largo de las secciones radiales, porque a lo largo de los arcos, la fuerza  y el corrimiento
y el corrimiento  son perpendiculares y en tales casos
son perpendiculares y en tales casos  es nulo. La suma del trabajo hecho en los segmentos radiales que constituyen la trayectoria II es el mismo que el trabajo efectuado en la trayectoria I, porque cada trayectoria está compuesta del mismo conjunto de segmentos radiales. Como la trayectoria II es arbitraria, se ha demostrado que el trabajo realizado es el mismo para todas las trayectorias que unen A con B.
es nulo. La suma del trabajo hecho en los segmentos radiales que constituyen la trayectoria II es el mismo que el trabajo efectuado en la trayectoria I, porque cada trayectoria está compuesta del mismo conjunto de segmentos radiales. Como la trayectoria II es arbitraria, se ha demostrado que el trabajo realizado es el mismo para todas las trayectorias que unen A con B.
Aun cuando esta prueba sólo es válida para el caso especial ilustrado en la figura, la diferencia de potencial es independiente de la trayectoria para dos puntos cualesquiera en cualquier campo eléctrico. Se desprende de ello el carácter conservativo de la interacción electrostática el cual está asociado a la naturaleza central de las fuerzas electrostáticas.
Para un par de placas paralelas en las cuales se cumple que 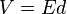 , donde d es la distancia entre las placas paralelas y E es el campo eléctrico constante en la región entre las placas.
, donde d es la distancia entre las placas paralelas y E es el campo eléctrico constante en la región entre las placas.
Campo eléctrico
El campo eléctrico es un campo físico que es representado mediante un modelo que describe la interacción entre cuerpos y sistemas con propiedades de naturaleza eléctrica.1 Se describe como un campo vectorial en el cual una carga eléctrica puntual de valor  sufre los efectos de una fuerza eléctrica
sufre los efectos de una fuerza eléctrica 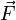 dada por la siguiente ecuación:
dada por la siguiente ecuación:
(1)
En los modelos relativistas actuales, el campo eléctrico se incorpora, junto con el campo magnético, en campo tensorialcuadridimensional, denominado campo electromagnético Fμν.2
Los campos eléctricos pueden tener su origen tanto en cargas eléctricas como en campos magnéticos variables. Las primeras descripciones de los fenómenos eléctricos, como la ley de Coulomb, sólo tenían en cuenta las cargas eléctricas, pero las investigaciones de Michael Faraday y los estudios posteriores de James Clerk Maxwell permitieron establecer las leyes completas en las que también se tiene en cuenta la variación del campo magnético.
Esta definición general indica que el campo no es directamente medible, sino que lo que es observable es su efecto sobre alguna carga colocada en su seno. La idea de campo eléctrico fue propuesta por Faraday al demostrar el principio de inducción electromagnética en el año 1832.
La unidad del campo eléctrico en el SI es Newton por Culombio (N/C), Voltio por metro (V/m) o, en unidades básicas, kg·m·s−3·A−1 y la ecuación dimensional es MLT-
Definición
La presencia de carga eléctrica en una región del espacio modifica las características de dicho espacio dando lugar a un campo eléctrico. Así pues, podemos considerar un campo eléctrico como una región del espacio cuyas propiedades han sido modificadas por la presencia de una carga eléctrica, de tal modo que al introducir en dicho campo eléctrico una nueva carga eléctrica, ésta experimentará una fuerza.
El campo eléctrico se representa matemáticamente mediante el vector campo eléctrico, definido como el cociente entre la fuerza eléctrica que experimenta una carga testigo y el valor de esa carga testigo (una carga testigo positiva).
La definición más intuitiva del campo eléctrico se la puede dar mediante la ley de Coulomb. Esta ley, una vez generalizada, permite expresar el campo entre distribuciones de carga en reposo relativo. Sin embargo, para cargas en movimiento se requiere una definición más formal y completa, se requiere el uso de cuadrivectores y el principio de mínima acción. A continuación se describen ambas.
Debe tenerse presente de todas maneras que desde el punto de vista relativista, la definición de campo eléctrico es relativa y no absoluta, ya que observadores en movimiento relativo entre sí medirán campos eléctricos o "partes eléctricas" del campo electromagnético diferentes, por lo que el campo eléctrico medido dependerá del sistema de referencia escogido.
Definición mediante la ley de Coulomb
Partiendo de la ley de Coulomb que expresa que la fuerza entre dos cargas en reposo relativo depende del cuadrado de la distancia, matemáticamente es igual a:1
Donde:
-
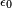 es la permisividad eléctrica del vacío, constante definida en el sistema internacional,
es la permisividad eléctrica del vacío, constante definida en el sistema internacional, -
 son las cargas que interactúan,
son las cargas que interactúan, -
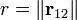 es la distancia entre ambas cargas,
es la distancia entre ambas cargas, -
 , es el vector de posición relativa de la carga 2 respecto a la carga 1.
, es el vector de posición relativa de la carga 2 respecto a la carga 1.
y  es el unitario en la dirección
es el unitario en la dirección 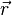 . Nótese que en la fórmula se está usando
. Nótese que en la fórmula se está usando 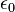 , esta es la permitividad en el vacío. Para calcular la interacción en otro medio es necesario cambiar la permitividad de dicho medio. (
, esta es la permitividad en el vacío. Para calcular la interacción en otro medio es necesario cambiar la permitividad de dicho medio. ( )
)
La ley anterior presuponía que la posición de una partícula en un instante dado, hace que su campo eléctrico afecte en el mismo instante a cualquier otra carga. Ese tipo de interacciones en las que el efecto sobre el resto de partículas parece depender sólo de la posición de la partícula causante sin importar la distancia entre las partículas se denomina en física acción a distancia. Si bien la noción de acción a distancia fue aceptada inicialmente por el propio Newton, experimentos más cuidados a lo largo del siglo XIX llevaron a desechar dicha noción como no-realista. En ese contexto se pensó que el campo eléctrico no sólo era un artificio matemático sino un ente físico que se propaga a una velocidad finita (la velocidad de la luz) hasta afectar a otras partículas. Esa idea conllevaba modificar la ley de Coulomb de acuerdo con los requerimientos de la teoría de la relatividad y dotar de entidad física al campo eléctrico.1 Así, el campo eléctrico es una distorsión electromagnética que sufre el espacio debido a la presencia de una carga. Considerando esto se puede obtener una expresión del campo eléctrico cuando este sólo depende de la distancia entre las cargas:
Donde claramente se tiene que  , la que es una de las definiciones más conocidas acerca del campo eléctrico.
, la que es una de las definiciones más conocidas acerca del campo eléctrico.
Definición formal
La definición más formal de campo eléctrico, válida también para cargas moviéndose a velocidades cercanas a la de la luz, surge a partir de calcular la acción de una partícula cargada en movimiento a través de un campo electromagnético.2 Este campo forma parte de un único campo electromagnético tensorial 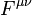 definido por un potencial cuadrivectorial de la forma:1
definido por un potencial cuadrivectorial de la forma:1
(1)
donde  es el potencial escalar y
es el potencial escalar y  es el potencial vectorial tridimensional. Así, de acuerdo al principio de mínima acción, se plantea para una partícula en movimiento en un espacio cuadridimensional:
es el potencial vectorial tridimensional. Así, de acuerdo al principio de mínima acción, se plantea para una partícula en movimiento en un espacio cuadridimensional:
(2)
donde  es la carga de la partícula,
es la carga de la partícula,  es su masa y
es su masa y  la velocidad de la luz. Reemplazando () en () y conociendo que
la velocidad de la luz. Reemplazando () en () y conociendo que  , donde
, donde 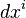 es el diferencial de la posición definida
es el diferencial de la posición definida  y
y  es la velocidad de la partícula, se obtiene:
es la velocidad de la partícula, se obtiene:
(3)
El término dentro de la integral se conoce como el lagrangiano del sistema; derivando esta expresión con respecto a la velocidad se obtiene el momento de la partícula, y aplicando lasecuaciones de Euler-Lagrange se encuentra que la variación temporal de la cantidad de movimiento de la partícula es:
(4)
De donde se obtiene la fuerza total de la partícula. Los dos primeros términos son independientes de la velocidad de la partícula, mientras que el último depende de ella. Entonces a los dos primeros se les asocia el campo eléctrico y al tercero el campo magnético. Así se encuentra la definición más general para el campo eléctrico:2
(5)
La ecuación () brinda mucha información acerca del campo eléctrico. Por un lado, el primer término indica que un campo eléctrico es producido por la variación temporal de un potencial vectorial descrito como 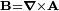 donde
donde  es el campo magnético; y por otro, el segundo representa la muy conocida descripción del campo como el gradiente de un potencial.2
es el campo magnético; y por otro, el segundo representa la muy conocida descripción del campo como el gradiente de un potencial.2
Descripción del campo eléctrico
Matemáticamente un campo se lo describe mediante dos de sus propiedades, su divergencia y su rotacional. La ecuación que describe la divergencia del campo eléctrico se la conoce como ley de Gauss y la de su rotacional es la ley de Faraday.1
Ley de Gauss
Para conocer una de las propiedades del campo eléctrico se estudia que ocurre con el flujo de éste al atravesar una superficie. El flujo de un campo  se obtiene de la siguiente manera:
se obtiene de la siguiente manera:
(8)
donde 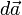 es el diferencial de área en dirección normal a la superficie. Aplicando la ecuación () en () y analizando el flujo a través de una superficie cerrada se encuentra que:
es el diferencial de área en dirección normal a la superficie. Aplicando la ecuación () en () y analizando el flujo a través de una superficie cerrada se encuentra que:
(9)
donde 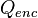 es la carga encerrada en esa superficie. La ecuación () es conocida como la ley integral de Gauss y su forma derivada es:
es la carga encerrada en esa superficie. La ecuación () es conocida como la ley integral de Gauss y su forma derivada es:
(10)
donde  es la densidad volumétrica de carga. Esto indica que el campo eléctrico diverge hacia una distribución de carga; en otras palabras, que el campo eléctrico comienza en una carga y termina en otra.1
es la densidad volumétrica de carga. Esto indica que el campo eléctrico diverge hacia una distribución de carga; en otras palabras, que el campo eléctrico comienza en una carga y termina en otra.1
Esta idea puede ser visualizada mediante el concepto de líneas de campo. Si se tiene una carga en un punto, el campo eléctrico estaría dirigido hacia la otra carga.
Ley de Faraday
En 1801, Michael Faraday realizó una serie de experimentos que lo llevaron a determinar que los cambios temporales en el campo magnético inducen un campo eléctrico. Esto se conoce como la ley de Faraday. La fuerza electromotriz, definida como el rotacional a través de un diferencial de línea está determinado por:
(11)
donde el signo menos indica la Ley de Lenz y  es el flujo magnético en una superficie, determinada por:
es el flujo magnético en una superficie, determinada por:
(12)
reemplazando () en () se obtiene la ecuación integral de la ley de Faraday:
(13)
Aplicando el teorema de Stokes se encuentra la forma diferencial:
(14)
La ecuación () completa la descripción del campo eléctrico, indicando que la variación temporal del campo magnético induce un campo eléctrico.1
Expresiones del campo eléctrico
Campo electrostático (cargas en reposo)
Un caso especial del campo eléctrico es el denominado electrostático. Un campo electrostático no depende del tiempo, es decir es estacionario. Para este tipo de campos la Ley de Gauss todavía tiene validez debido a que esta no tiene ninguna consideración temporal, sin embargo, la Ley de Faraday debe ser modificada. Si el campo es estacionario, la parte derecha de la ecuación () y () no tiene sentido, por lo que se anula:
(15)
Esta ecuación junto con () definen un campo electrostático. Además, por el cálculo diferencial, se sabe que un campo cuyo rotacional es cero puede ser descrito mediante el gradiente de una función escalar  , conocida como potencial eléctrico:
, conocida como potencial eléctrico:
(16)
La importancia de () radica en que debido a que el rotacional del campo eléctrico es cero, se puede aplicar el principio de superposición a este tipo de campos. Para varias cargas, se define el campo eléctrico como la suma vectorial de sus campos individuales:
(17)
entonces
(18)
Líneas de campo
Un campo eléctrico estático puede ser representado geométricamente con líneas tales que en cada punto el campo vectorial seatangente a dichas líneas, a estas líneas se las conoce como "líneas de campo". Matemáticamente las líneas de campo son las curvas integrales del campo vectorial. Las líneas de campo se utilizan para crear una representación gráfica del campo, y pueden ser tantas como sea necesario visualizar.
Las líneas de campo son líneas perpendiculares a la superficie del cuerpo, de manera que su tangente geométrica en un punto coincide con la dirección del campo en ese punto. Esto es una consecuencia directa de la ley de Gauss, es decir encontramos que la mayor variación direccional en el campo se dirige perpendicularmente a la carga. Al unir los puntos en los que el campo eléctrico es de igual magnitud, se obtiene lo que se conoce como superficies equipotenciales, son aquellas donde el potencial tiene el mismo valor numérico. En el caso estático al ser el campo eléctrico un campo irrotacional las líneas de campo nunca serán cerradas (cosa que sí puede suceder en el caso dinámico, donde el rotacional del campo eléctrico es igual a la variación temporal del campo magnético cambiada de signo, por tanto una línea de campo eléctrico cerrado requiere un campo magnético variable, cosa imposible en el caso estático).
En el caso dinámico pueden definirse igualmente las líneas sólo que el patrón de líneas variará de un instante a otro del tiempo, es decir, las líneas de campo al igual que las cargas serán móviles.
Campo electrodinámico (movimiento uniforme)
El campo eléctrico creado por una carga puntual presenta isotropía espacial, en cambio, el campo creado por una carga en movimiento tiene un campo más intenso en el plano perpendicular a la velocidad de acuerdo a las predicciones de la teoría de la relatividad. Esto sucede porque para un observador en reposo respecto a una carga que se mueve con velocidad uniforme la distancia en la dirección del movimiento de la carga serán menores que las medidas por un observador en reposo respecto a la carga, por efecto de la contracción de Lorentz, suponiendo que la carga se mueve a lo largo del eje X de observador tendríamos la siguiente relación de coordenadas entre lo medido por el observador en movimiento respecto a la carga  y el observador en reposo respecto a la carga
y el observador en reposo respecto a la carga 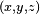 :
:
Siendo V la velocidad de la carga respecto al observador, así la distancia efectiva a la carga medida por el observador en movimiento respecto a la carga cumplirá que:
Y por tanto el campo eléctrico medido por un observador en movimiento respecto a la carga será:
(19)
Donde  es el ángulo formado por el vector de posición del punto donde se mide el campo (respecto a la carga) y la velocidad del movimiento. De esta última expresión se observa que si se considera una esfera de radio r alrededor de la carga el campo es más intenso en el "ecuador", tomando como polos norte y sur la interasección de la esfera con la trayectoria de la partícula, puede verse que el campo sobre la esfera varía entre un máximo
es el ángulo formado por el vector de posición del punto donde se mide el campo (respecto a la carga) y la velocidad del movimiento. De esta última expresión se observa que si se considera una esfera de radio r alrededor de la carga el campo es más intenso en el "ecuador", tomando como polos norte y sur la interasección de la esfera con la trayectoria de la partícula, puede verse que el campo sobre la esfera varía entre un máximo  y un mínimo
y un mínimo  dados por:
dados por:
(20)
Esta pérdida de simetría esférica es poco notoria para velocidades pequeñas comparadas con la velocidad de la luz y se hace muy marcada a velocidades cercanas a la luz.
Campo electrodinámico (movimiento acelerado)
El campo de una carga en movimiento respecto a un observador se complica notablemente respecto al caso de movimiento uniforme si además de un movimiento relativo la carga presenta un movimiento acelerado respecto a un observador inercial. A partir de los potenciales de Lienard-Wiechert se obtiene que el campo creado por una carga en movimiento viene dado por:
(21)
El primer miembro sólo depende de la velocidad y coincide con el campo eléctrico provocado por una carga en movimiento uniforme, a grandes distancias varía según una ley de la inversa del cuadrado 1/R2 y, por tanto, no supone emisión de energía, el segundo miembro depende de la aceleración  y tiene una variación 1/R que representa la intensidad decreciente de una onda esférica de radiación electromagnética, ya que las cargas en movimiento acelerado emiten radiación.
y tiene una variación 1/R que representa la intensidad decreciente de una onda esférica de radiación electromagnética, ya que las cargas en movimiento acelerado emiten radiación.
Energía del campo eléctrico
Un campo en general almacena energía y en el caso de cargas aceleradas puede transmitir también energía (principio aprovechado en antenas de telecomunicaciones). La densidad volumétrica de energía de un campo eléctrico está dada por la expresión siguiente:1
(22)
Por lo que la energía total en un volumen V está dada por:
(23)
donde 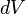 es el diferencial de volumen.
es el diferencial de volumen.
CORRIENTE ELECTRICA
La corriente eléctrica o intensidad eléctrica es el flujo de carga eléctrica por unidad de tiempo que recorre un material. 1 Se debe al movimiento de las cargas (normalmente electrones) en el interior del material. En el Sistema Internacional de Unidades se expresa en C/s (culombios sobre segundo), unidad que se denomina amperio. Una corriente eléctrica, puesto que se trata de un movimiento de cargas, produce un campo magnético, un fenómeno que puede aprovecharse en el electroimán.
El instrumento usado para medir la intensidad de la corriente eléctrica es el galvanómetro que, calibrado en amperios, se llamaamperímetro, colocado en serie con el conductor cuya intensidad se desea medir.


Leyenda:
1. Electrones
2. Sensor o sonda Hall
3. Imanes
4. Campo magnético
5. Fuente de energía
Descripción
En la imagen A, una carga negativa aparece en el borde superior del sensor Hall (simbolizada con el color azul), y una positiva en el borde inferior (color rojo). En B y C, el campo eléctrico o el magnético están invertidos, causando que la polaridad se invierta. Invertir tanto la corriente como el campo magnético (imagen D) causa que la sonda asuma de nuevo una carga negativa en la esquina superior.
Se le llama resistencia eléctrica a la igualdad de oposición que tienen los electrones para desplazarse a través de un conductor. La unidad de resistencia en el Sistema Internacional es el ohmio, que se representa con la letra griega omega (Ω), en honor al físico alemán George Ohm, quien descubrió el principio que ahora lleva su nombre. La resistencia está dada por la siguiente fórmula:
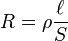
En donde ρ es el coeficiente de proporcionalidad o la resistividad del material.

Símbolo de la resistencia eléctrica en uncircuito.
La resistencia de un material depende directamente de dicho coeficiente, además es directamente proporcional a su longitud (aumenta conforme es mayor su longitud) y es inversamente proporcional a su sección transversal (disminuye conforme aumenta su grosor o sección transversal)
Descubierta por Georg Ohm en 1827, la resistencia eléctrica tiene un parecido conceptual a la fricción en la física mecánica. La unidad de la resistencia en el Sistema Internacional de Unidadeses el ohmio (Ω). Para su medición, en la práctica existen diversos métodos, entre los que se encuentra el uso de un ohmnímetro. Además, su cantidad recíproca es la conductancia, medida enSiemens.
Además, de acuerdo con la ley de Ohm la resistencia de un material puede definirse como la razón entre la diferencia de potencial eléctrico y la corriente en que atraviesa dicha resistencia, así:1

Donde R es la resistencia en ohmios, V es la diferencia de potencial en voltios e I es la intensidad de corriente en amperios.
También puede decirse que "la intensidad de la corriente que pasa por un conductor es directamente proporcional a la longitud e inversamente proporcional a su resistencia"
Según sea la magnitud de esta medida, los materiales se pueden clasificar en conductores, aislantes y semiconductor. Existen además ciertos materiales en los que, en determinadas condiciones de temperatura, aparece un fenómeno denominado superconductividad, en el que el valor de la resistencia es prácticamente nulo.
Comportamientos ideales y reales
Una resistencia ideal es un elemento pasivo que disipa energía en forma de calor según la ley de Joule]]. También establece una relación de proporcionalidad entre la intensidad de corriente que la atraviesa y la tensión medible entre sus extremos, relación conocida como ley de Ohm:
donde i(t) es la corriente eléctrica que atraviesa la resistencia de valor R y u(t) es la diferencia de potencial que se origina. En general, una resistencia real podrá tener diferente comportamiento en función del tipo de corriente que circule por ella.
Comportamiento en corriente continua
Una resistencia real en corriente continua (CC) se comporta prácticamente de la misma forma que si fuera ideal, esto es, transformando la energía eléctrica en calor por efecto Joule. La ley de Ohm para corriente continua establece que:
donde R es la resistencia en ohmios, V es la diferencia de potencial en voltios e I es la intensidad de corriente en amperios.
Comportamiento en corriente alterna
Como se ha comentado anteriormente, una resistencia real muestra un comportamiento diferente del que se observaría en una resistencia ideal si la intensidad que la atraviesa no es continua. En el caso de que la señal aplicada sea senoidal, corriente alterna (CA), a bajas frecuencias se observa que una resistencia real se comportará de forma muy similar a como lo haría en CC, siendo despreciables las diferencias. En altas frecuencias el comportamiento es diferente, aumentando en la medida en la que aumenta la frecuencia aplicada, lo que se explica fundamentalmente por los efectos inductivos que producen los materiales que conforman la resistencia real.
Por ejemplo, en una resistencia de carbón los efectos inductivos solo provienen de los propios terminales de conexión del dispositivo mientras que en una resistencia de tipo bobinado estos efectos se incrementan por el devanado de hilo resistivo alrededor del soporte cerámico, además de aparecer una cierta componente capacitiva si la frecuencia es especialmente elevada. En estos casos, para analizar los circuitos, la resistencia real se sustituye por una asociación serie formada por una resistencia ideal y por una bobina también ideal, aunque a veces también se les puede añadir un pequeño condensador ideal en paralelo con dicha asociación serie. En los conductores, además, aparecen otros efectos entre los que cabe destacar el efecto pelicular.
Consideremos una resistencia R, como la de la figura 2, a la que se aplica una tensión alterna de valor:
De acuerdo con la ley de Ohm circulará una corriente alterna de valor:
donde  . Se obtiene así, para la corriente, una función senoidal que está en fase con la tensión aplicada (figura 3).
. Se obtiene así, para la corriente, una función senoidal que está en fase con la tensión aplicada (figura 3).
Si se representa el valor eficaz de la corriente obtenida en forma polar:
Y operando matemáticamente:
De donde se deduce que en los circuitos de CA la resistencia puede considerarse como una magnitud compleja con parte real y sin parte imaginaria o, lo que es lo mismo con argumento nulo, cuya representación binómica y polar serán:
Ley de Ohm
La ley de Ohm dice que la intensidad de la corriente que circula entre dos puntos de un circuito eléctrico es proporcional a la tensión eléctrica entre dichos puntos. Esta constante es la conductancia eléctrica, que es la inversa de la resistencia eléctrica.
La intensidad de corriente que circula por un circuito dado es directamente proporcional a la tensión aplicada e inversamente proporcional a la resistencia del mismo. Cabe recordar que esta ley es una propiedad específica de ciertos materiales y no es una ley general del electromagnetismo como la ley de Gauss, por ejemplo.
Introducción
La ecuación matemática que describe esta relación es:
Donde, I es la corriente que pasa a través del objeto en amperios, V es la diferencia de potencial de las terminales del objeto en voltios, G es la conductancia en siemens y R es la resistencia enohmios (Ω). Específicamente, la ley de Ohm dice que R en esta relación es constante, independientemente de la corriente.1
Esta ley tiene el nombre del físico alemán Georg Ohm, que en un tratado publicado en 1827, halló valores de tensión y corriente que pasaba a través de unos circuitos eléctricos simples que contenían una gran cantidad de cables. Él presentó una ecuación un poco más compleja que la mencionada anteriormente para explicar sus resultados experimentales. La ecuación de arriba es la forma moderna de la ley de Ohm.
Esta ley se cumple para circuitos y tramos de circuitos pasivos que, o bien no tienen cargas inductivas ni capacitivas (únicamente tiene cargas resistivas), o bien han alcanzado un régimen permanente (véase también «Circuito RLC» y «Régimen transitorio (electrónica)»). También debe tenerse en cuenta que el valor de la resistencia de un conductor puede ser influido por la temperatura.






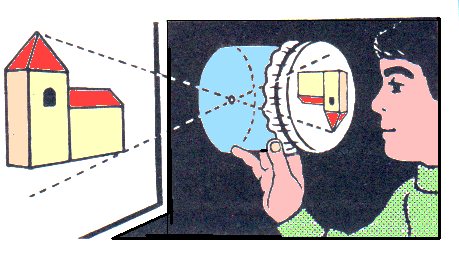



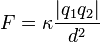






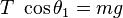
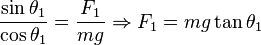

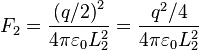



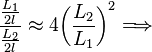
![\frac{L_1}{L_2}\approx 4 {\left ( \frac {L_2}{L_1} \right ) }^2\Longrightarrow \frac{L_1}{L_2}\approx\sqrt[3]{4} \,\!](https://upload.wikimedia.org/math/7/c/e/7cef359a7cd4a5f6a3be9d150a4a14e0.png)
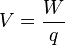


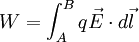







 .
.
 por una distribución de carga
por una distribución de carga  en forma de diferencial de línea (
en forma de diferencial de línea (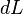 ), lo que produce un campo eléctrico
), lo que produce un campo eléctrico  .
.


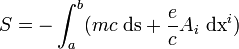
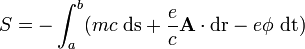










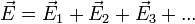






![\bold{E} = \frac{1}{4\pi\epsilon} \left[
\frac{q(1-\frac{v^2}{c^2})}{(r-\frac{\bold{r}\cdot\bold{v}}{c})^3}(\bold{r}-\frac{\bold{v}}{c}r) +
\frac{q}{c^2(R-\frac{\bold{r}\cdot\bold{v}}{c})^3} \left[ \bold{r}
\times \left( (\bold{r}-\frac{\bold{v}}{c}r) \times \dot{\bold{v}} \right) \right]
\right]](https://upload.wikimedia.org/math/8/c/b/8cb721fac4318c480449c45573f049cc.png)